Soliton:
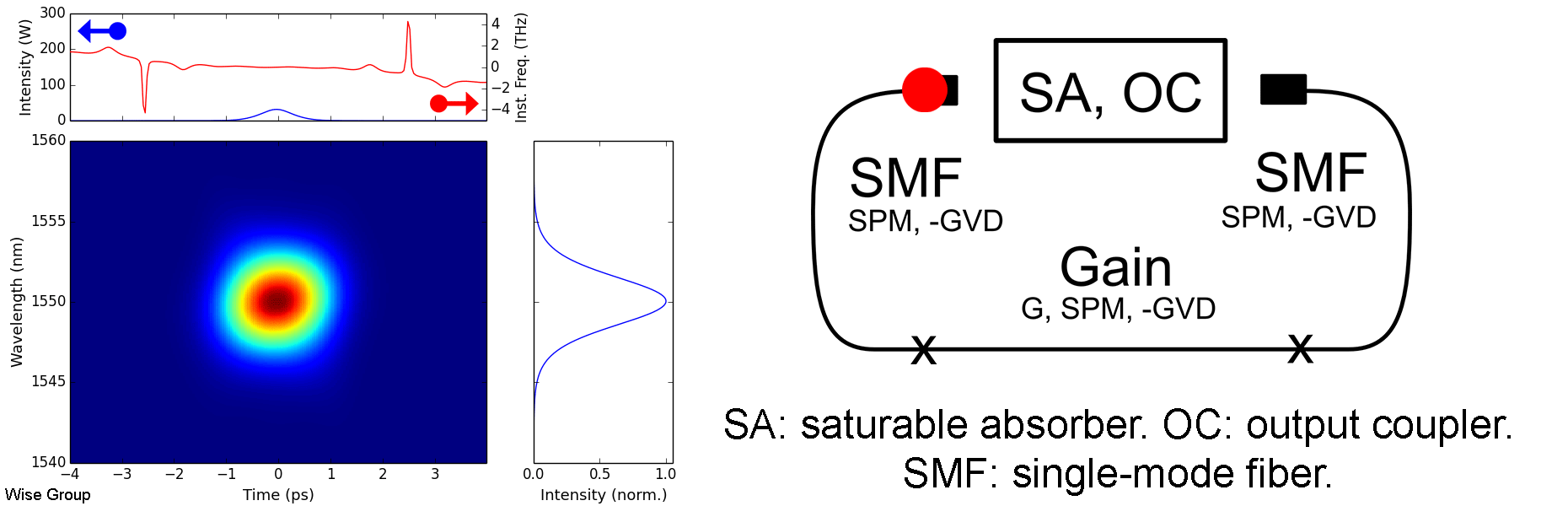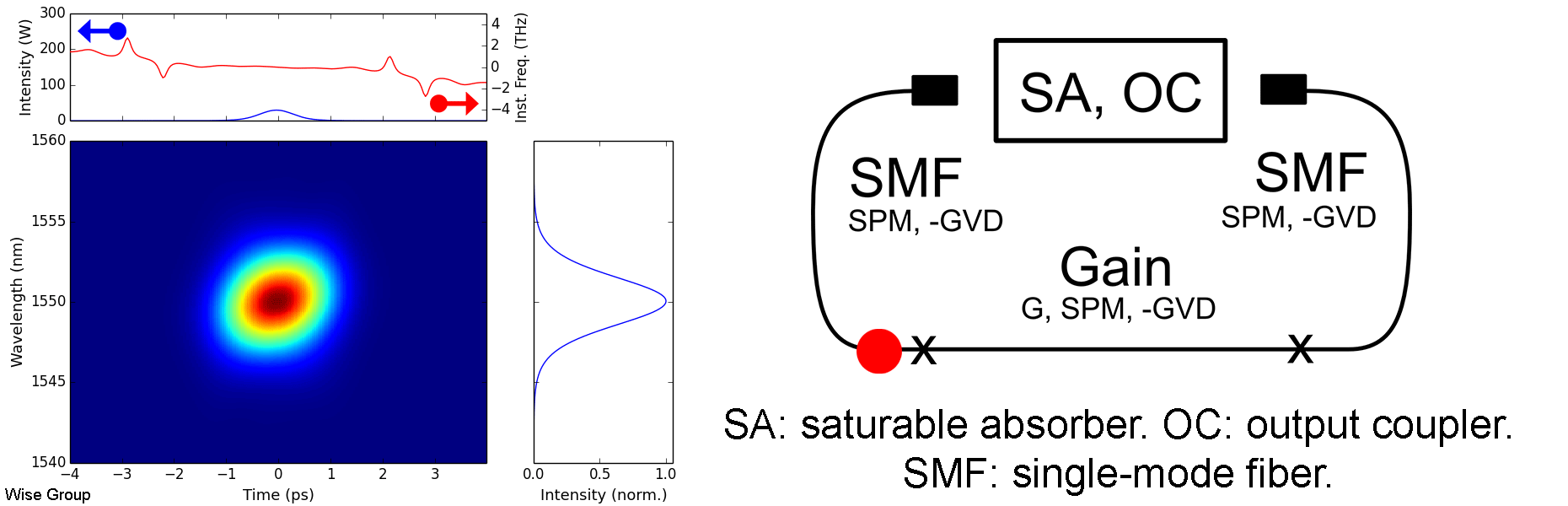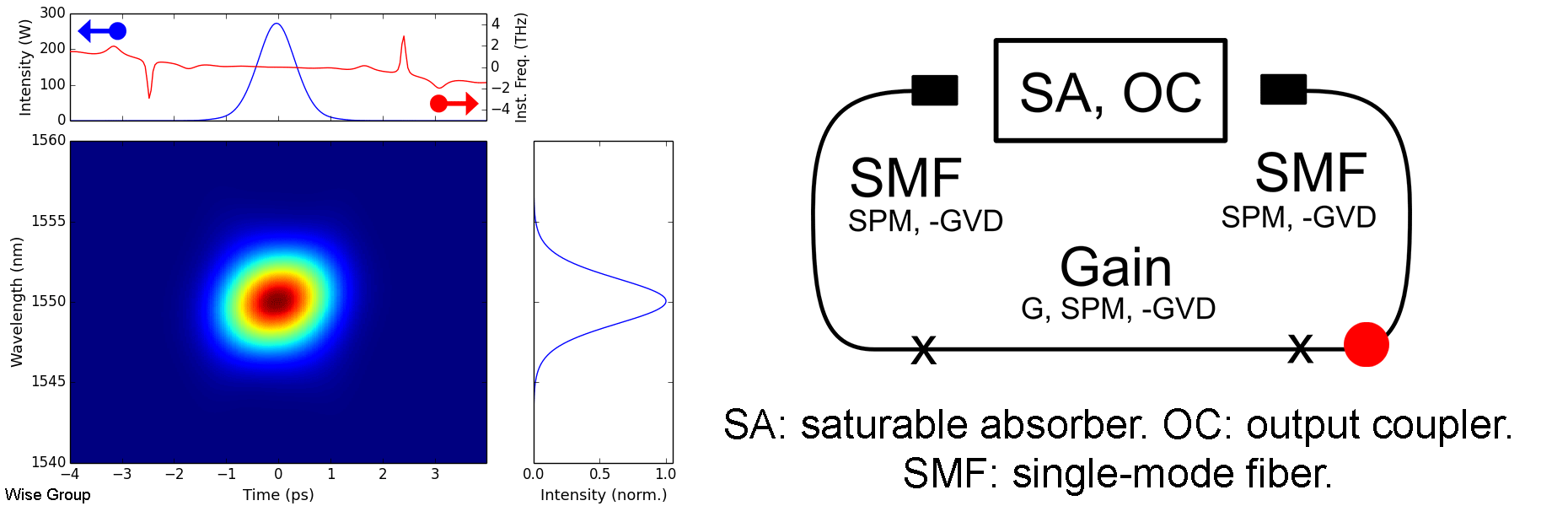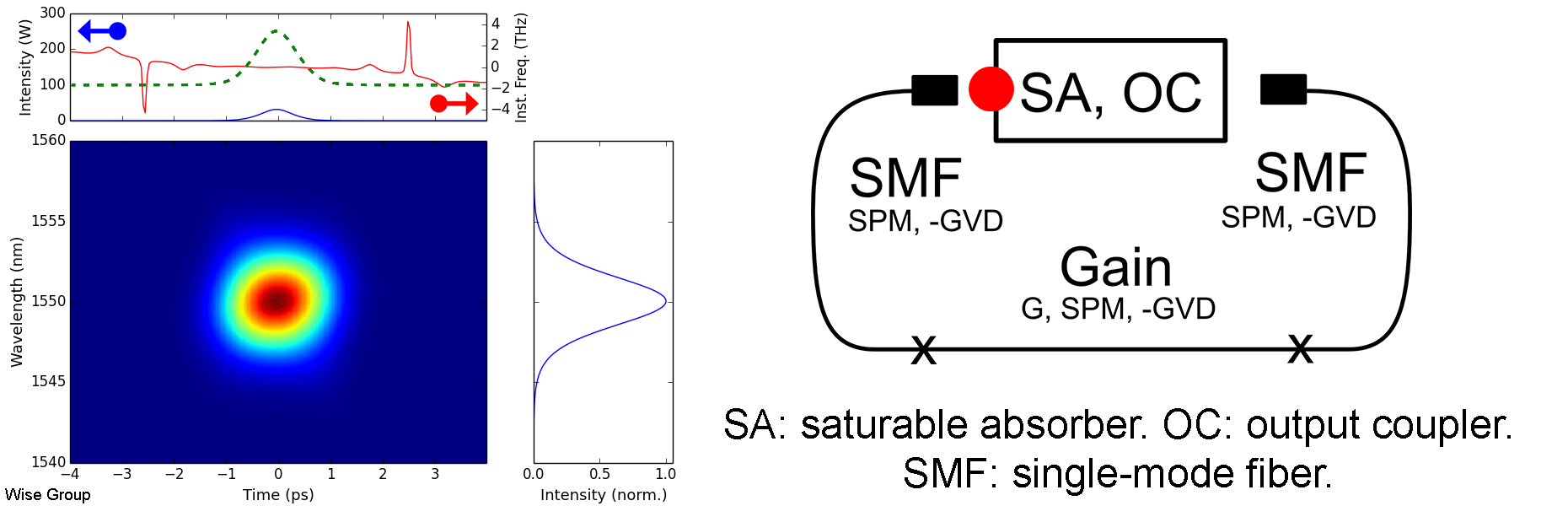
Overview of Evolution:
Pulse evolves to a soliton under nonlinearity and anomalous GVD. Pulse is more-or-less static and transform limited throughout each roundtrip.
Cavity Design:
Significantly anomalous net dispersion. An intra-cavity spectral filter may be useful for reducing resonant sidebands, and may permit easy wavelength tuning. Adjusting the cavity dispersion at fixed pulse energy yields various pulse durations, as per the soliton area theorem.
Soliton oscillators can be very simple, and output nearly transform-limited pulses. However, pulse durations are limited by the resonant instability Lcav≤(pi/2)LD, empirically observable as the growth of narrow spectral sidebands. In conjunction with the soliton area theorem, this also limits pulse energies, leading to typical performances of ~100 pJ and ~200 fs.
As the pulse circulates, it is periodically perturbed by the cavity’s discrete gain and loss elements. Following each such perturbation, the pulse adjusts itself to once more satisfy the soliton area theorem, in the process shedding some energy as a dispersive wave. As these dispersive waves continue to co-propagate with the pulse, any component with the same wave vector as the soliton will be resonantly amplified during subsequent roundtrips. This phenomenon is analogous to quasi-phase-matching in optical parametric amplifiers, and is responsible for the distinctive, narrowband, Kelly sidebands that appear in many soliton fiber lasers. Large Kelly sidebands are associated with lasers operating near the limits of their pulse energy, duration, and stability.
Solitons such as these are solutions to the nonlinear Schrodinger equation in anomalous dispersion. Balancing the effects of dispersion and Kerr nonlinearity leads to a family of possible solutions, described by the soliton area theorem; the specific member of this family that is observed in a cavity is determined by the dissipative effects of gain, loss, saturable absorption, and spectral filtering (if applicable). Despite this, we underscore that these dissipative effects remain only of secondary importance in soliton lasers, in contrast with dissipative soliton lasers, where they are of comparable importance to conservative effects such as dispersion and Kerr nonlinearity.
Related Papers:
1. I. N. Duling, III. “Subpicosecond all-fibre erbium laser.” Electronics Letters 27, 6 (1991).
2. I. N. Duling, III. “All-fiber soliton laser mode locked with a nonlinear mirror.” Optics Letters 16, 8 (1991).
3. J. P. Gordon. “Dispersive perturbations of solitons of the nonlinear Schrödinger equation.” Journal of the Optical Society of America B 9, 1 (1992).
4. G. P. Agrawal. Nonlinear Fiber Optics, Third Edition. Academic Press (2007).
5. G. P. Agrawal. Applications of Nonlinear Fiber Optics. Academic Press (2007).
Animation credit: Walter Fu.