Intro to HCFs
Hollow-core fibers have a different light-guiding mechanism than solid-core fibers due to their cores having the lowest indices caused by vacuum or gases. The most basic type of hollow-core fibers is capillaries, but they are not effective in guiding light with high bend loss. However, the use of special coatings or lossy waveguide modes can help to reduce the loss without bending. Another type of hollow-core fiber is the hollow-core photonic crystal fiber (HC-PCF), which uses photonic bandgap and anti-resonance mechanisms to guide light. Each type of fiber has its own advantages and disadvantages, with capillaries being cost-effective but limited, and HC-PCFs being more advanced but complex and costly to produce.
Capillary:
Capillary is probably the first hollow-core fiber used in gas-based nonlinear optics. It has a simple structure of a hollow core and a homogeneous solid cladding [1]. To make it more applicable, various coatings have been applied to further reduce propagating loss, such as cyclic olefin polymer [2] and AgI/Ag [3]. Due to its inability to guide light, it suffers from a significant amount of bend loss; thus, it requires ultimate straightness, regardless of its length, which adds to the complexity of using it. In addition, Capillary has high loss at small core radius, while a large core size restricts its usability only to a very high power level for the desired nonlinear effect to occur. Furthermore, during pulse propagation, higher-order modes in a large-core capillary can participate and complicate the nonlinear dynamics.
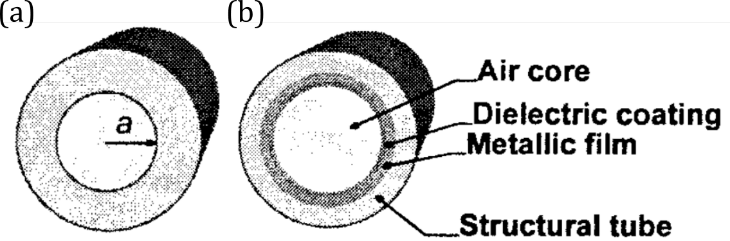
Capillaries without (a) and with (b) any coating. The coating can be metallic or dielectric to reduce the propagating loss [4].
Photonic bandgap fiber:
Photonic bandgap fiber features a hollow core that is enclosed by a honeycomb cladding structure with a substantial air-to-glass ratio. The periodic cladding structure produces a photonic bandgap that causes light to exist as an evanescent wave in the cladding if its wavelengths and axial wavevector components fall within a bandgap. However, if the light is localized to a defect of the periodic structure, namely the hollow core, it can propagate non-evanescently [5]. Nevertheless, its transmission bandwidth is restricted due to the limited size of the bandgap. Additionally, its dispersion profile is highly oscillatory, which may pose an issue in ultrafast nonlinear optics research.

SEM image of a PBGF [6].
Kagome fiber:
Kagome fiber derives the Japanese name from its particular lattice shape. Although its underlying guiding mechanism is still an active research, lots of numerical studies have attributed its origin to anti-resonances [7–9]. Its transmission band is interspaced by strong loss peaks that arise from the resonances between the core mode and the cladding walls.
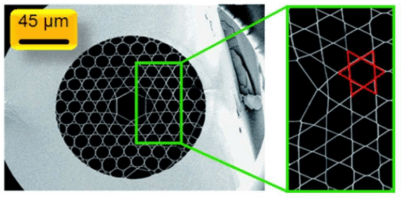
SEM image of a Kagome fiber [6].
Anti-Resonant fiber:
Research on anti-resonances and Kagome fibers led to the development of negative-curvature fibers whose cladding consists of only a single layer of tubes. Both anti-resonance and inhibited coupling contribute to the low loss in this type of fibers. Anti-resonance prevents light from leaking through a glass wall. Inhibited coupling results from a wavevector mismatch between the core mode and the cladding modes primarily residing inside a glass tube. With these effects, they have achieved a remarkably low loss as low as 10 dB/km [10]. A record low loss of 0.28 dB/km from 1510 to 1600 nm has also been demonstrated in nested anti-resonant fibers [11].
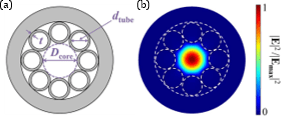
Schematic of an anti-resonant negative-curvature fiber [12]
[1] E. A. J. Marcatili and R. A. Schmeltzer, “Hollow metallic and dielectric waveguides for long distance optical transmission and lasers”, Bell Syst. Tech. J. 43, 1783–1809 (1964).
[2] Y.-W. Shi, K. Ito, L. Ma, T. Yoshida, Y. Matsuura, and M. Miyagi, “Fabrication of a polymer-coated silver hollow optical fiber with high performance”, Appl. Opt. 45, 6736–6740 (2006).
[3] K.-R. Sui, Y.-W. Shi, X.-L. Tang, X.-S. Zhu, K. Iwai, and M. Miyagi, “Optical properties of AgI/Ag infrared hollow fiber in the visible wavelength region”, Opt. Lett. 33, 318–320 (2008).
[4] J. A. Harrington, “A Review of IR Transmitting, Hollow Waveguides”, Fiber Integr. Opt. 19, 211–227 (2000).
[5] R. F. Cregan, B. J. Mangan, J. C. Knight, T. A. Birks, P. St. J. Russell, P. J. Roberts, and D. C. Allan, “Single-Mode Photonic Band Gap Guidance of Light in Air”, Science 285, 1537–1539 (1999).
[6] F. Belli, “Ultrafast Raman scattering in gas-filled hollow-core fibers”, PhD thesis (Friedrich-Alexander-Universit¨at Erlangen-N ¨ urnberg, 2017).
[7] G. J. Pearce, G. S. Wiederhecker, C. G. Poulton, S. Burger, and P. St. J. Russell, “Models for guidance in kagome-structured hollow-core photonic crystal fibres”, Opt. Express 15, 12680–12685 (2007).
[8] A. Argyros and J. Pla, “Hollow-core polymer fibres with a kagome lattice: potential for transmission in the infrared”, Opt. Express 15, 7713–7719 (2007).
[9] S. Fevrier, B. Beaudou, and P. Viale, “Understanding origin of loss in large pitch hollow-core photonic crystal fibers and their design simplification”, Opt. Express 18, 5142–5150 (2010).
[10] B. Debord, A. Amsanpally, M. Chafer, A. Baz, M. Maurel, J. M. Blondy, E. Hugonnot, F. Scol, L. Vincetti, F. Gerome, and F. Benabid, “Ultralow transmission loss in inhibited-coupling guiding hollow fibers”, Optica 4, 209–217 (2017).
[11] G. T. Jasion, T. D. Bradley, K. Harrington, H. Sakr, Y. Chen, E. N. Fokoua, I. A. Davidson, A. Taranta, J. R. Hayes, D. J. Richardson, and F. Poletti, “Hollow Core NANF with 0.28 dB/km Attenuation in the C and L Bands”, in Optical fiber communication conference postdeadline papers (2020), Th4B.4.
[12] C. Wei, R. J.Weiblen, C. R. Menyuk, and J. Hu, “Negative curvature fibers”, Adv. Opt. Photon. 9, 504–561 (2017).