Dissipative Soliton:
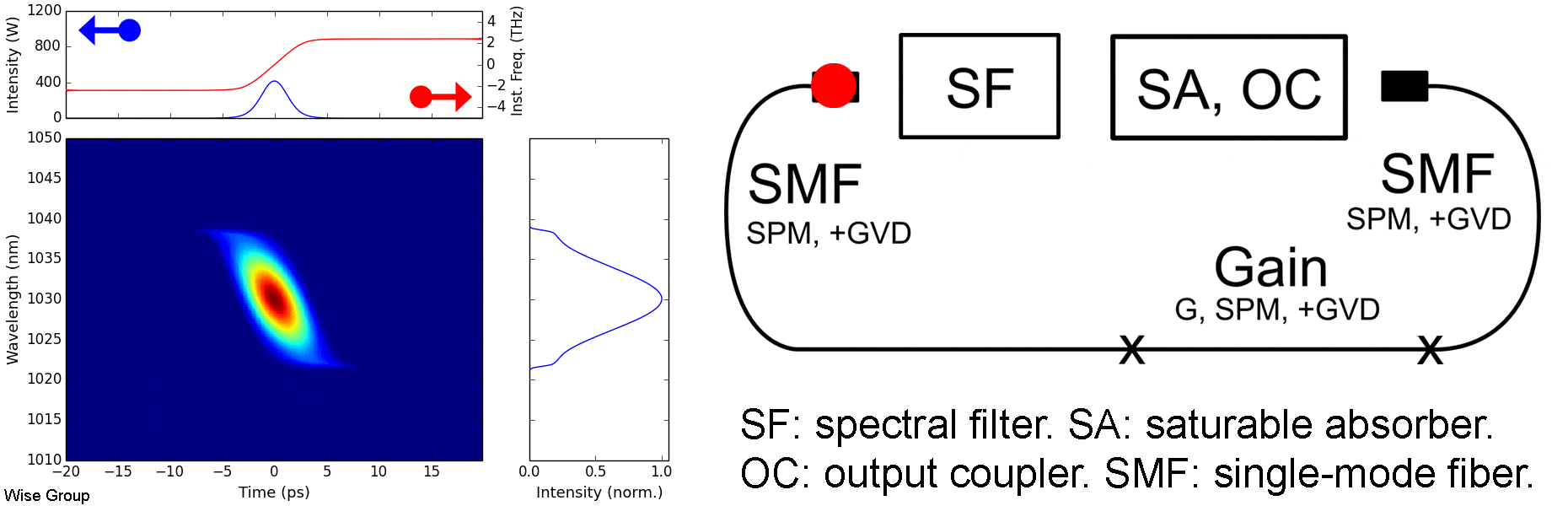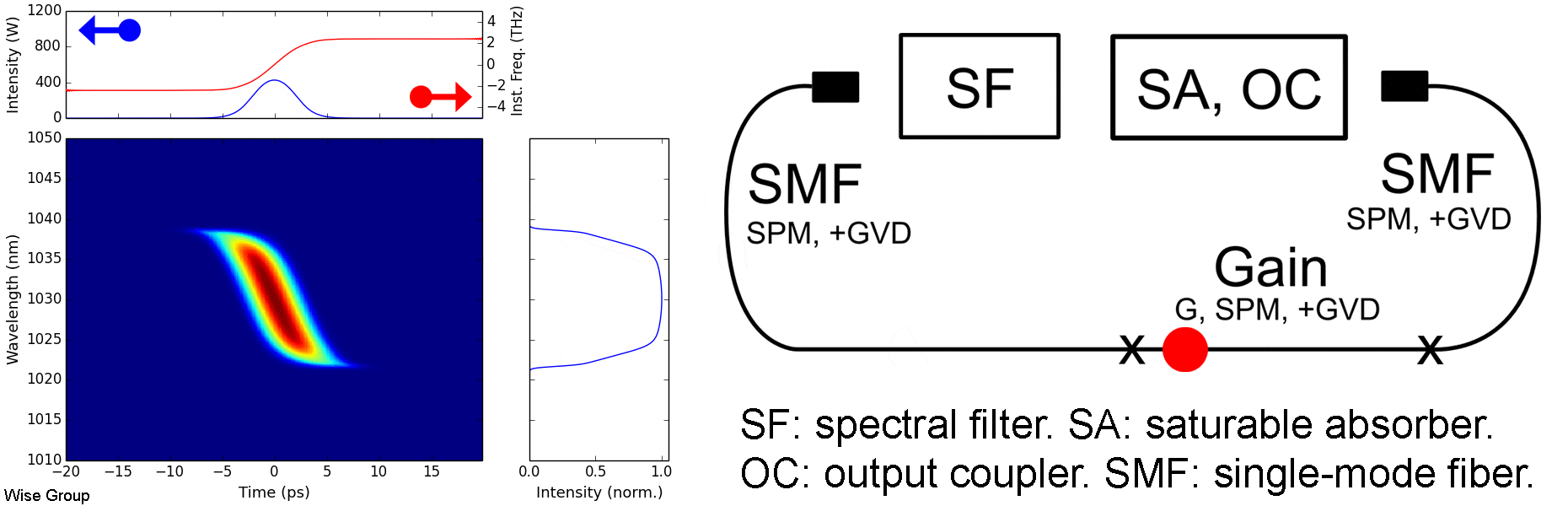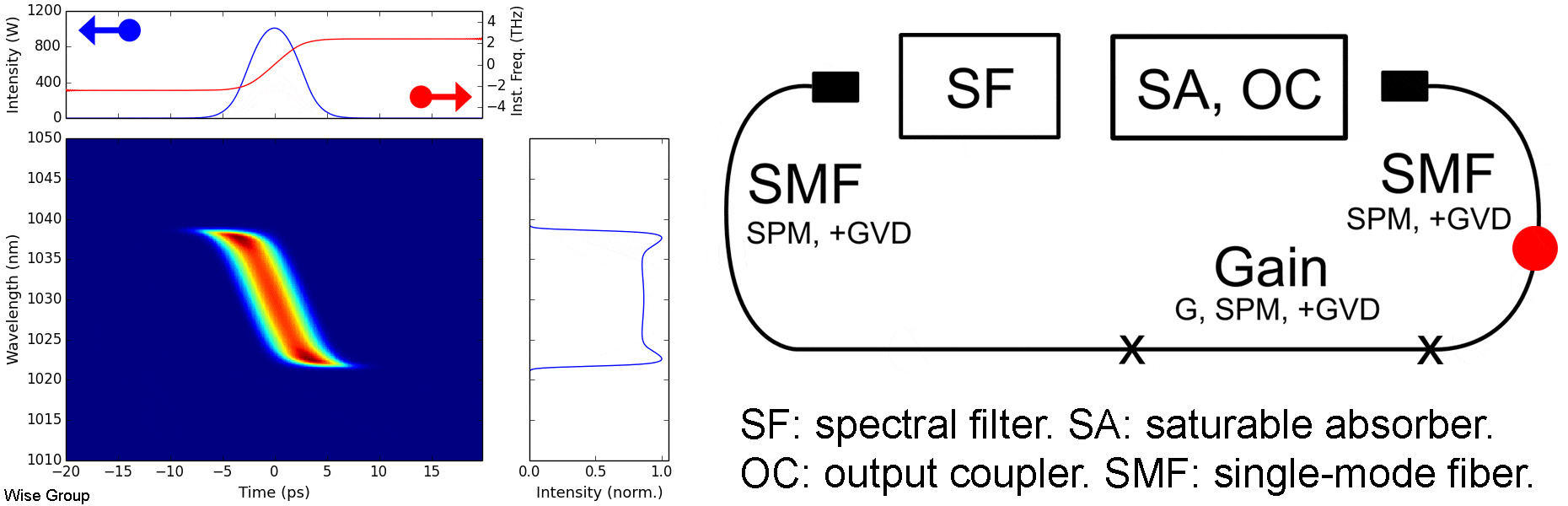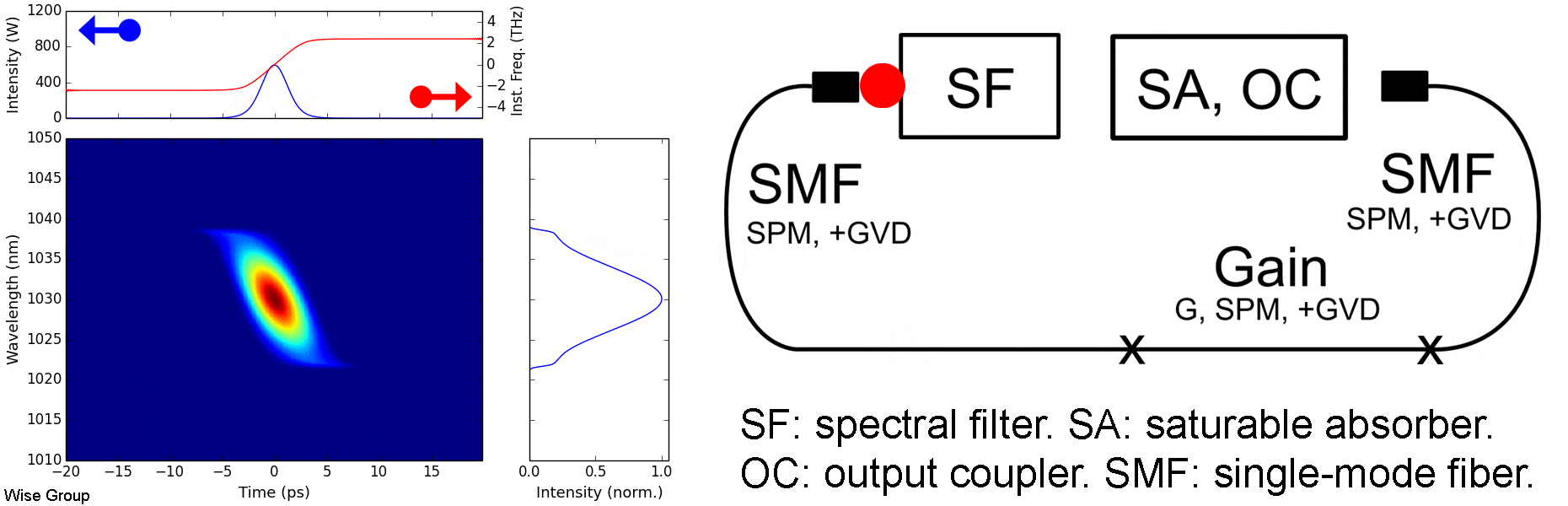
Overview of Evolution:
Pulse is highly up-chirped throughout the cavity. In both the temporal and spectral domains, the pulse broadens in normally-dispersive fiber and is then narrowed by a spectral filter, effecting modelocking.
Cavity Design:
All-normal-dispersion (ANDi) oscillators often yield the highest-energy pulses. A prototypical cavity comprises a normally-dispersive passive fiber followed by gain and another, shorter, passive fiber. After the output coupler, a spectral filter forms the feedback loop, with a width typically on the order of 10 nm at 1030 nm. The pulse energy is largely controlled by the filter bandwidth and the cavity dispersion, with more dispersive cavities requiring narrower filters. The output is a highly up-chirped pulse often with a distinctive steep, cat-ear spectrum.
This pulse evolution should not be confused with either the active or passive self-similar regimes. Features which distinguish it are the large chirp (with optimal compression typically requiring a GDD of several times the cavity dispersion); the tanh-like frequency sweep; and the lack of parabolic shaping effects in the time domain (see animation above).
In spite of their sharp spectral features, dissipative solitons can usually be compressed to within 20% of the transform limit with low secondary structure.
Pulses generally top out at ~20 nJ in ~200 fs, and improvement in one aspect is possible with compromises in the other. Optimizing for duration can yield sub-100 fs pulses at the few-nJ level, while giant chirp oscillators represent the opposite limit.
It is worthwhile to clarify that when we speak of dissipative solitons here, we are referring specifically to solutions of the complex cubic-quintic Ginzburg-Landau equation (CQGLE) in normal dispersion, where dissipative effects such as the spectral filter and saturable absorber are of comparable importance to conservative effects such as dispersion and Kerr nonlinearity. This terminology emphasizes the contrast with, for instance, conservative solitons of the nonlinear Schrodinger equation.
Related Papers:
1. A. Chong, J. Buckley, W. H. Renninger, and F. W. Wise. “All-normal-dispersion femtosecond fiber laser.” Optics Express 14, 21 (2006).
2. A. Chong, W. H. Renninger, and F. W. Wise. “All-normal-dispersion femtosecond fiber laser with pulse energy above 20 nJ.” Optics Letters 32, 16 (2007).
3. A. Chong, W. H. Renninger, and F. W. Wise. “Properties of normal-dispersion femtosecond fiber lasers.” Journal of the Optical Society of America B 25, 2 (2008).
4. K. Kieu, W. H. Renninger, A. Chong, and F. W. Wise. “Sub-100 fs pulses at watt-level powers from a dissipative-soliton fiber laser.” Optics Letters 34, 5 (2009).
5. P. Grelu and N. Akhmediev. “Dissipative solitons for mode-locked lasers.” Nature Photonics 6, 2 (2012).
Animation credit: Walter Fu.