Raman scattering regimes
The nonlinear effects driven by the Raman response strongly depend on the pump pulse duration relative to both the period of the molecular oscillations TR (inversely proportional to the Raman transition frequency) and their dephasing time T2. Raman-induced index change underlies such nonlinear dynamics and is a good indicator for explaining and distinguishing different regimes of Raman physics. Since the index change is proportional to coherence, molecular oscillations are commonly referred to as coherence waves or phonon waves. Raman dephasing time is thus equivalent to the phonon decay time.
In general, there are three regimes of Raman scattering according to the response of permittivity to the field. Below we briefly list a few properties they have.
Impulsive regime (pulse duration<TR, T2>>pulse duration and TR):
The pulse is short enough to impulsively excite the Raman scattering and induce an index modulation that follows an almost-undamped sinusoidal wave. The sinusoidal index modulation allows for a nonlocal coherent interaction between two temporally-separated pulses [1].
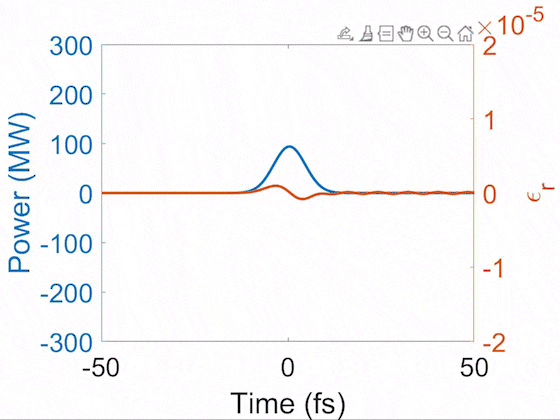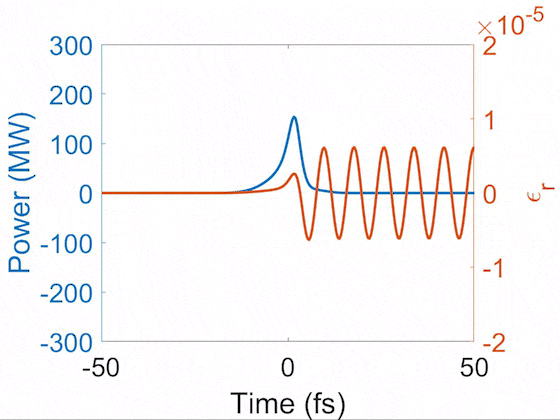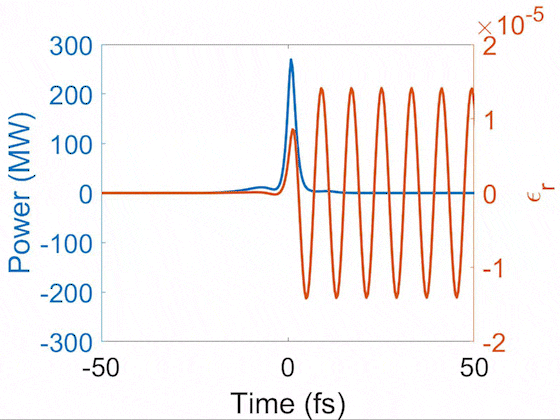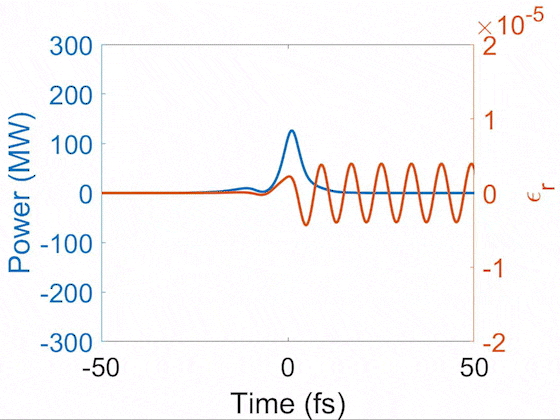
Evolution of pulse temporal profile (blue) and Raman-induced index modulation (orange). This demonstrates the soliton self-compression where the pulse is shortened nonlinearly during propagation. After it is shortened below the Raman cycle, it enters the impulsive Raman regime and thus drives the sinusoidal index modulation. Here, a 10-fs pulse is shortened to 2 fs, driving the vibrational SRS in H2 that has a 8-fs cycle.
In general, gases have long dephasing times, so their index modulations continue to ring for a long time. There are several patterns of index modulations resulting from interference of phonon waves. Below we show the impulsively-excited index modulations from N2, O2, and H2.
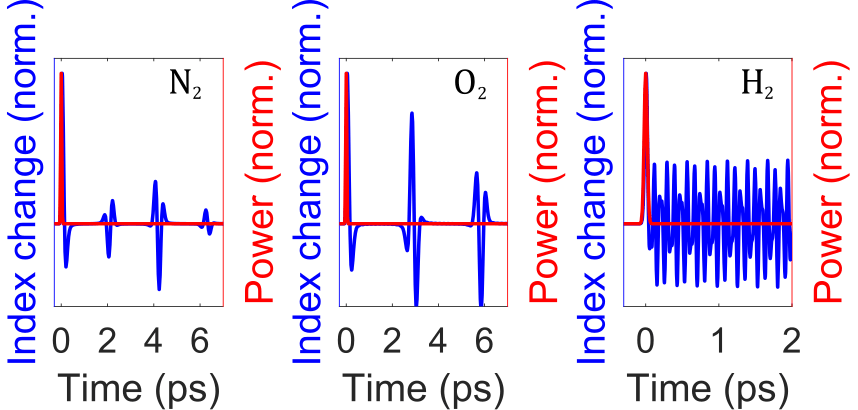
Transient regime (pulse duration>TR, , T2>>pulse duration and TR):
Here, the permittivity change follows the field, which resembles the Kerr electronic response. Since the electronic response in gases is weak, this Raman-induced Kerr effect contributes significantly to an enhanced effective Kerr nonlinearity and leads to an enhancement of the soliton self-compression [2] and spectral broadening during SRS [3] in H2.
In addition to the Raman-enhanced Kerr effect, the Raman-Stokes pulse generated in the transient regime has a phase that is copied from the pump pulse; that is to say, the coherent property is transferred to the Raman-Stokes pulse. This property of coherent tranfer allows for the generation of ultrashort Raman generation with an ultrashort pump pulse. The phase copy from the pump to the Stokes field underlies the SPM-induced Raman suppression. Strong SPM is known to suppress SRS in the transient Raman regime due to phase mismatch [4]. Besides, a long-lasting Raman response implies that Raman generation depends on the pulse energy [5-7].
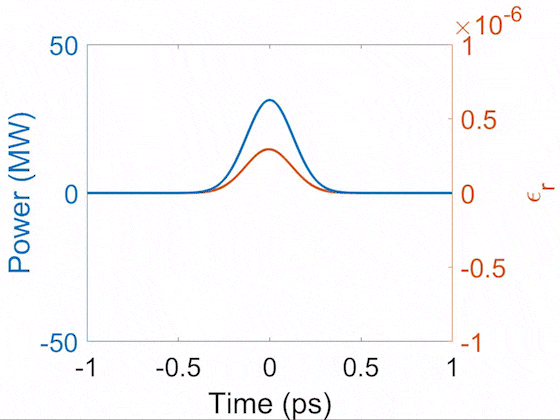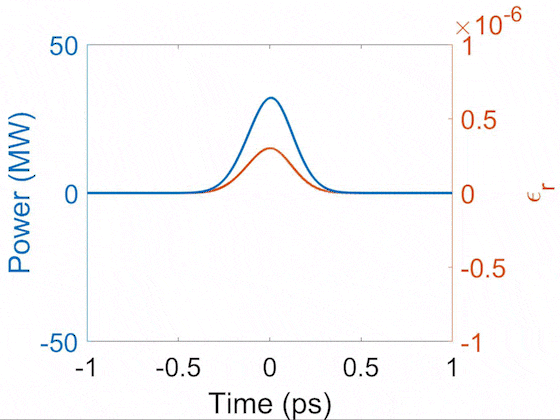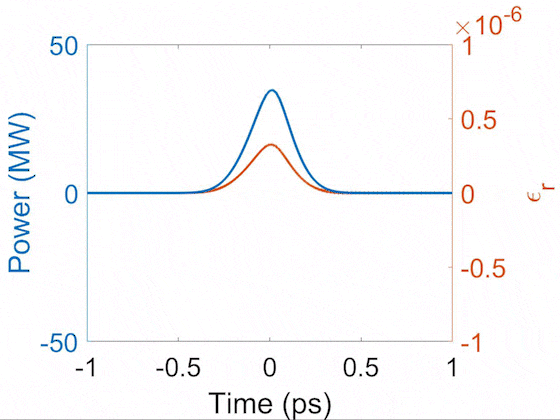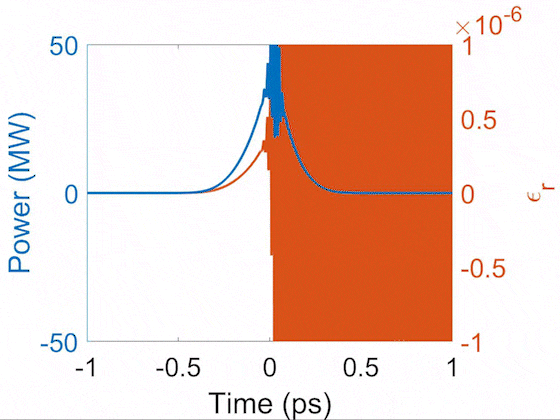
Evolution of pulse temporal profile (blue) and Raman-induced index modulation (orange). This demonstrates that the Raman-induced index follows the shape of the pulse in the transient regime. During the propagation, the Raman Stokes signal grows and beats with the pump, creating short peaks which drive the impulsive-Raman sinusoidal index modulation.
Steady-state regime (pulse duration>T2):
In contrast to the pump-Stokes coherent phase transfer in the transient regime, the Stokes field in the steady-state Raman regime, which is common in silica-based solid-core fibers, does not inherit the phase from the pump. Its phonons dissipate too fast compared to the pulse duration; therefore, the Raman generation depends only on the instantaneous pump intensity. If the Stokes seed results from spontaneous Raman scattering and is thus noisy, each temporal slice of a Stokes pulse exhibits a different phase due to the noisy seed growing independently.
To model the Raman effect, we have derived the analytical equations in the supplement of our papers [8,9].
[1] F. Belli, A. Abdolvand, J. C. Travers, and P. St. J. Russell, “Control of ultrafast pulses in a hydrogen-filled hollow-core photonic-crystal fiber by Raman coherence”, Phys. Rev. A 97, 013814 (2018).
[2] F. Belli, A. Abdolvand, W. Chang, J. C. Travers, and P. St. J. Russell, “Vacuum-ultraviolet to infrared supercontinuum in hydrogen-filled photonic crystal fiber”, Optica 2, 292–300 (2015).
[3] L. L. Losev, “Spectral broadening of femtosecond pulses during SRS in hydrogen”, Laser Phys. Lett. 19, 095402 (2022).
[4] A. V. Konyashchenko, P. V. Kostryukov, L. L. Losev, and V. S. Pazyuk, “Minimum possible laser pulse duration for SRS”, Quantum Electron. 47, 593–596 (2017).
[5] R. L. Carman, F. Shimizu, C. S. Wang, and N. Bloembergen, “Theory of Stokes Pulse Shapes in Transient Stimulated Raman Scattering”, Phys. Rev. A 2, 60–72 (1970).
[6] M. D. Duncan, R. Mahon, L. L. Tankersley, and J. Reintjes, “Transient stimulated Raman amplification in hydrogen”, J. Opt. Soc. Am. B 5, 37–52 (1988).
[7] P. Hosseini, D. Novoa, A. Abdolvand, and P. St. J. Russell, “Enhanced Control of Transient Raman Scattering Using Buffered Hydrogen in Hollow-Core Photonic Crystal Fibers”, Phys. Rev. Lett. 119, 253903 (2017).
[8] Y.-H. Chen, P. Sidorenko, E. Antonio-Lopez, R. Amezcua-Correa, and F. W. Wise, “Efficient soliton self-frequency shift in hydrogen-filled hollow-core fiber”, Opt. Lett. 47, 285–288 (2022).
[9] Y.-H. Chen, J. Moses, F. Wise, “Femtosecond long-wave-infrared generation in hydrogen-filled hollow-core fiber”, J. Opt. Soc. Am. B (2023)